[成果] Multiagent model and mean field theory of complex auction dynamics
来源:
作者:陈清华
发布时间:2015-09-07
浏览次数:
由我院陈清华副教授、王有贵教授和亚利桑那州立大学来颖诚教授、兰州大学黄子罡教授合作研究的“Multiagent model and mean field theory of complex auction dynamics”已被《New Journal of Physics》接受并于9月2日刊出。

长期以来,学者对于最小唯一拍卖的研究主要立足于完美信息下的Nash均衡框架,从结果上很难对真实的投标分布情况做出好的解释,特别是在实证投标分布中的增长部分。此外,从逻辑上看,完美信息的Nash均衡所需要的假设很强,实际情况难以满足。所以需要寻找另外的框架来进行讨论这个问题。
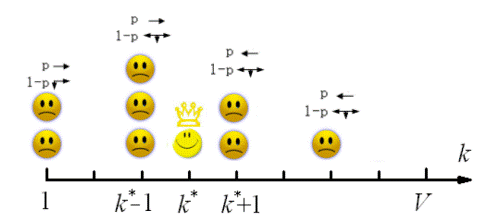
文章提出了一个具有学习效应的多主体模型,物理上可以看作多个粒子在一定随机驱动情况下的有界范围内的随机行走。模型框架如下图所示,每个个体以一定的概率p向胜利者前进一步(多步也可以,或者某一个分布);1-p的概率进行随机行走。个体的投标是离散的并被限制在一个有限区间(不能比1小,不能比标的物品的价格V多)。
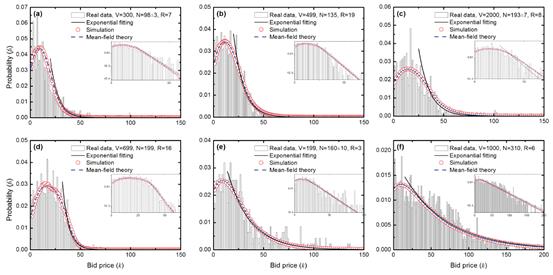
无论初始的投标分布如何,经过足够长的时间后系统会达到一个相当稳定的动态平衡。我们进行了平均场分析得到了和多个体模拟一致的结果,还证明了尾段的指数下降现象(这个现象在一些实证工作的文章中被提及而没有解决)。理论和实证结果的比较如下图,图中灰色柱状图为实际分布,红圈为多个体模型模拟的结果,蓝色虚线为平均场分析结果,黑色实线是对实证数据尾部的指数拟合。相比以前的模型,文章提出的向胜利者学习的机制显得更加合理(向更高收益者学习是人类的基本行为模式),并且该假设从实际数据的分析中获得支持(感谢Filippo Radicchi所提供的数据)。最后还值得突出说明的是,模型只有一个参数(学习率p),但获得了更好的整体拟合效果。
注:和传统的“价高者得之”的拍卖方式不同,最小唯一拍卖是一种比较新颖的拍卖方式,所有唯一出价中最小的获胜。这种拍卖中的投标分布会呈现倒J形模式,并且这种特征非常显著,如何解释这个分布的形成吸引了学者的关注。我院陈清华副教授和王有贵教授及其合作者近几年对这种分布的形成进行了深入的研究,提出了几种可能的机制模型,相比以前的工作与实际分布的拟合效果更好,而机制更加合理。具体可以参考如下已经发表的文献:
1 Yinan Zhao, Qinghua Chen, Yougui Wang (2013) Bid distribution derived from consistent mixed strategy in lowest unique bid auction. International Journal of Modern Physics C 25: 1440002.
2 C Zhou, H Dong, R Hu, Q Chen (2015) Smarter than Others? Conjectures in Lowest Unique Bid Auctions. PLoS ONE 10(4): e0122923. doi:10.1371/journal.pone.0122923 (http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0122923)
3 Qinghua Chen, Zi-Gang Huang, Yougui Wang and Ying-Cheng Lai (2015) Multi-agent model and mean field theory of complex auction dynamics. New Journal of Physics, 17: 093003. doi:10.1088/1367-2630/17/9/093003
(http://iopscience.iop.org/article/10.1088/1367-2630/17/9/093003)