什么是复杂系统?
部分摘自《地理元胞自动机研究》一书第一章(有改动),部分张江撰稿
什么是复杂系统?也许你会说:具有复杂性的系统,就是复杂系统,而简单的系统就不是复杂系统。然而事实可能远没有这么简单,请尝试回答下面的几个问题:
飞鸟是如何聚集成群的?蚂蚁如何形成王国?为什么冷战结束,世界反而硝烟四起?为什么苏联以及东欧等一系列社会主义国家会在1989年的几个月内轰然坍塌?生命是如何起源的?计算机病毒具有生命么?为什么在1998年爆发了亚洲经济风暴,进而导致全球的经济危机?大脑是什么?感情、思想、目的和意识这样不可言喻的特征是如何产生的?难道大脑仅仅是简单的随机进化的结果么?
这些问题看似不是什么科学的问题,然而它们都有一个共同点,就是属于同一种系统,既复杂系统。
首先,复杂系统是相对牛顿时代以来构成科学事业焦点的简单系统相比而言的,两者具有根本性的不同。简单系统通常具有少量个体对象,它们之间的相互作用比较弱,或者具有大量相近行为的个体,比如封闭的气体或遥远的星系,以至于我们能够应用简单的统计平均的方法来研究它们的行为。而复杂并不一定与系统的规模成正比,复杂系统要有一定的规模,但也不是越大越复杂。另外复杂系统中的个体一般来讲具有一定的智能性,例如组织中的细胞、股市中的股民、城市交通系统中的司机、生态系统中的动植物……,这些个体都可以根据自身所处的部分环境通过自己的规则进行智能的判断或决策。
根据以上的描述,我们可以得到复杂性科学中对复杂系统的描述性定义:复杂系统是具有中等数目基于局部信息做出行动的智能性、自适应性主体的系统。根据这个定义,我们不难总结出复杂系统的以下几个核心的特点:
(1)中等大小数目的主体,通俗的讲也就是元素不能少,也不能太多。对于一般的系统我们可以按照系统内个体的数目以及相互作用的强度进行分类,得到下面的图:


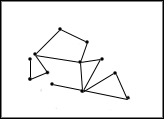
a)简单系统 b)无组织的复杂系统 c)有组织的复杂系统
说明:
a)简单系统,特点是元素数目特别少,因此可以用较少的变数来描述,这种系统可以用牛顿力学去加以解析。
b)无组织的“复杂”系统:其特征是元素和变量数很多,但其间的耦合是微弱的,或随机的,即只能用统计的方法去分析。热力学研究的对象一般就是这样的系统。
c)有组织的复杂系统:特征是元素数目很多,且其间存在着强烈的耦合作用。
复杂性科学所感兴趣的正是最后一种有组织的复杂系统。因为对于第一种系统来说,传统的牛顿力学范式的分析方法已经给出了这类系统行为的很好的解释。而对于第二类系统,由于其元素数目太多,必然是元素间的耦合“失去”个性,从而能够用统计方法去研究,成为一种简单的系统。所以,复杂系统的元素并不是多数就复杂,只用具有中等数目大小的系统才是一个有趣的系统,也才是一个复杂的系统。
(2)智能性和自适应性:这意味着系统内的元素或主体的行为遵循一定的规则,根据“环境”和接收信息来调整自身的状态和行为,并且主体通常有能力来根据各种信息调整规则,产生以前从未有过的新规则。通过系统主体的相对低等的智能行为,系统在整体上显现出更高层次、更加复杂、更加协调职能的有序性。
(3)局部信息,没有中央控制:在复杂系统中,没有哪个主体能够知道其他所有主体的状态和行为,每个主题只可以从个体集合的一个相对较小的集合中获取信息,处理“局部信息”,做出相应的决策。系统的整体行为是通过个体之间的相互竞争、协作等局部相互作用而涌现出来的。最新研究表明,在一个蚂蚁王国中,每一个蚂蚁并不是根据“国王”的命令来统一行动,而是根据同伴的行为以及环境调整自身行为,而是先一个有机的群体行为。
另外,复杂系统还具有突现性、不稳性、非线性、不确定性、不可预测性等等特征。面对这样的复杂系统,人们是如何进行分析和研究的呢?一种方法是利用计算机仿真的方法通过模拟复杂系统中个体的行为,让一群这样的个体在计算机所营造的虚拟环境下进行相互作用并演化,从而让整体系统的复杂性行为自下而上的“涌现”出来。这就是圣塔菲(Santa Fe)研究所研究复杂系统的主要方法。我们不妨称这种方法为自下而上的“涌现”方法。另一方面,人脑面对复杂系统可以通过有限的理性和一些不确定信息做出合理的决策,得到满意的结果,因此,研究人脑面对复杂系统是如何解决问题的则是另一种“自上而下”的解决问题的方法,我们不妨称这种方法为“控制”方法。下面我们用经济系统举例说明这两种方法的差异。
我们知道,经济系统是一个复杂系统,每一个人就构成了系统的元素,他们根据自己的决策规则选择合适的时机进行买卖经济活动。按照“涌现”的方法来研究这样的系统,就是要在计算机上实现一个模拟的交易市场,并且创造若干相互买卖的虚拟“人”,每个“人”都用计算机编好的规则进行买卖的决策,虽然现实中的人用到的决策规则远远比计算机模型中的“人”的模型复杂的多,但是这样的近似还是有意义的,因为当若干这样的个体组合在一起构成系统的时候,宏观经济系统的一些现象就会自下而上的“涌现”出来,这些涌现出来的现象在很多方面还是客观反映真实经济系统的。
按照“控制”的观点,我们可以通过找到几个宏观经济系统的指标量,比如GDP、价格指数、失业率等等,然后根据这些经济指标累计学习系统运作的规律,通过一段时间内系统的运作,我们不难积累一些经验,这些经验就可以构成描述经济系统运作的规则。然后,我们就可以按照找寻出来的经济系统的规则对经济系统进行控制,例如通过政府的政策来改变经济系统中每个个体的决策环境和制度环境来改变个体的行为规则,从而改变整个宏观经济系统的运行状况。在这里需要指出的是,宏观经济规律的把握并不破坏复杂系统中局部信息的性质,因为对于经济系统的规律把握是在高于经济系统个体层次的基础上进行的。我们可以认为政府具有这种高层次的性质,也就是说它不是严格意义上的经济系统中的主体。
我们看到上面两种方法都可以有效的对复杂系统进行把握,然而他们用的方法是完全不一样的。目前,大部分复杂性科学研究复杂系统的时候都用的是“涌现”的方法。而对于“控制”的方法实际上在人工智能学科诞生的时候已经开始使用了,例如专家系统的实践,各种逻辑系统的仿真都是使用这种自上而下的方法完成的,而将这种方法用于复杂系统的研究则很少提及。在这里,我们分两部分介绍研究复杂系统的这两种方法。
另外,非线性系统科学虽然不属于复杂性科学范畴(正相反,复杂系统一般都是非线性系统),但是由于在方法论和思想上两种体系具有很多相似性,因此在这里我们也一并介绍。


