分形网络的可控性 Controllability of fractal networks: An analytical approach
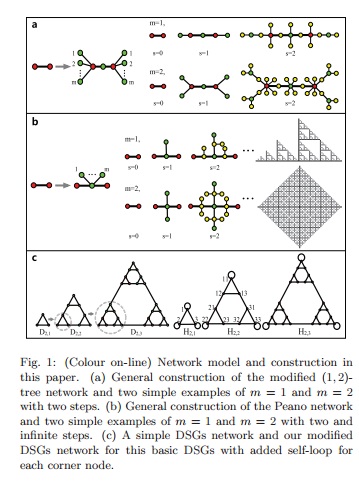
利用已有的复杂网络严格可控相关结论,理论推导和分析了三类规则分形网络的严格可控性问题。分别给出了三类规则分形网络满足严格可控性需要的最少控制输入个数的理论表达式,进一步给出在网络极限情形下控制输入个数的结论。
研究成果:
Jingwen Li et al 2014 EPL 105 58001 doi:10.1209/0295-5075/105/58001
Controllability of fractal networks: An analytical approach
Jingwen Li1, Zhengzhong Yuan1,2, Ying Fan1, Wen-Xu Wang1 and Zengru Di1
Show affiliationsLetter
Fractal networks are ubiquitous in nature, ranging from river networks to vascular networks. The ultimate goal of exploring these fractal networked systems lies in controlling the dynamical processes that take place on them. We offer analytical results to exactly understand our ability to control the dynamics of regular fractal networks in terms of identifying the minimum number of driver nodes that are required to achieve full control. According to the exact controllability theory, the controllability of an undirected network is completely determined by the eigenvalue spectrum of the coupling matrix that captures the network structure. The self-similarity in the fractal networks allows us to solve exactly the eigenvalue spectrum from the growth unit and the steps of the iterations, enabling an analytical quantification of the controllability of the fractal networks via the eigenvalue spectrum. We validate our exact analytical results in three typical regular fractal networks. Our results have implications for the control of many real networked systems that have fractal characteristics.
原文链接:
http://iopscience.iop.org/0295-5075/105/5/58001


