Games on graphs: A minor modification of payoff scheme makes a big difference

Qiang Zhang, Tianxiao Qi, Keqiang Li, Zengru Di and Jinshan Wu^(a)

School of Systems Science, Beijing Normal University - 100875 Beijing PRC 

^(a) jinshanw@bnu.edu.cn

Received: 3 March 2014
Accepted: 11 June 2014

Abstract

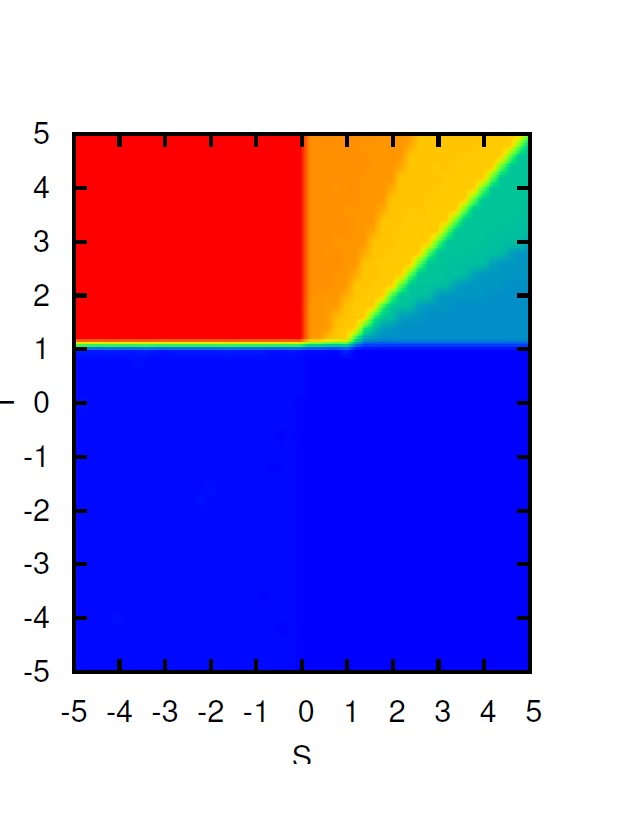
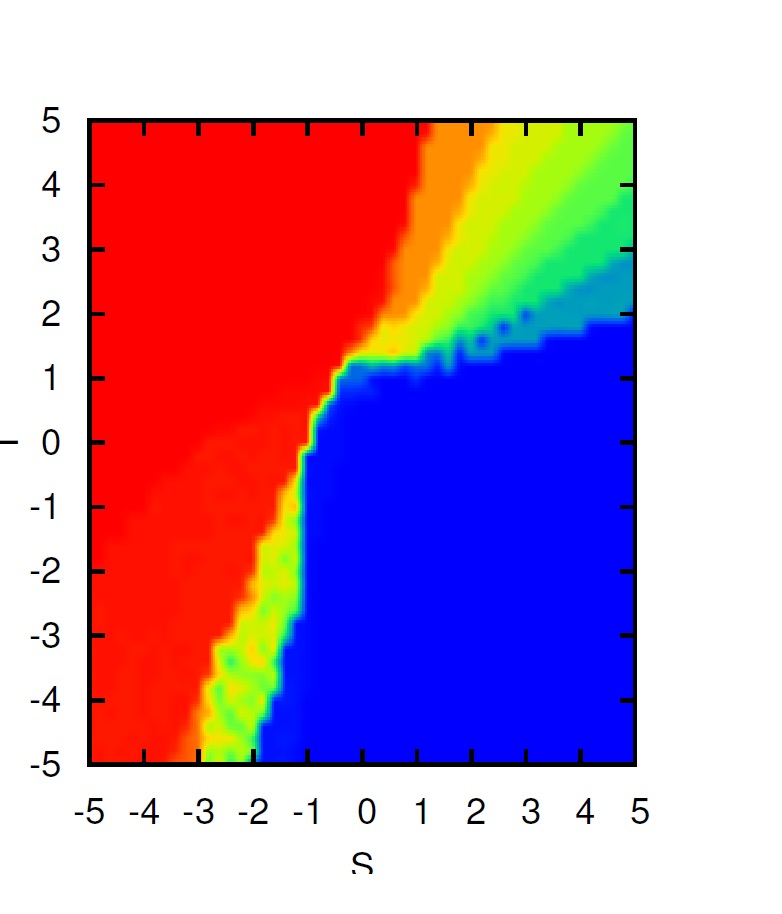
Many techniques developed in simulations of physical models have been adopted in studies of game theory by researchers including physicists and mathematicians. In this work, we show that a seemingly non-essential mechanism —what we refer to as a “payoff scheme”— has a large impact on strategic outcomes of some games. The payoff scheme here refers to how each player's payoff is calculated in each round after the states of all of the players are determined. Conventionally either the accumulated or the average payoff of a player is used, where its payoff is calculated from pairing up the player with all of its neighboring players. Here we consider to calculate the payoff from pairing up with only one random player from the neighboring players. The average payoff scheme that involves averaging over all of the neighbors should, in a sense, be equivalent to repeatedly randomly pairing up with one neighbor a time, which we refer to as the stochastic payoff scheme. However, our simulation of games on graphs shows that, in many cases, the two payoff schemes lead to qualitatively different levels of cooperation: Seemingly non-essential modifications might have large impact on behavioral outcomes. We have also observed that results from the stochastic scheme are more robust than the average scheme: different updating rules and initial states of the players do not have a large impact on the final level of cooperation in the former case when compared with those in the latter case.