研究成果：Sun, W., Zeng, A. European Physical Journal B (2017). doi: 10.1140/epjb/e2016-70618-0

简介：复杂网络的抗毁性在各个领域都是重要的话题。许多工作都致力于评估且提高复杂网络在面对攻击时的稳定性。最近，如何恢复遭受攻击后的网络被广泛地研究。现有的方法主要针对网络整体功能的修复，然而在许多实际情况中应优先修复网络中的重要节点，我们把这些情况下的修复称为靶向修复。比如，对于受寒潮影响而瘫痪的网络，靶向修复将会修复那些能使人口密集城市的交通最快恢复的节点。在这篇文章中，我们首先比较了攻击对整个网络和对靶向节点的影响，接着研究了基于全局中心性指标的传统修复方法的修复效果。更多的，基于靶向中心性，我们引入了局域介数修复方法并且发现此方法的修复效果要优于传统方法。最终，我们提出了一个包含局域介数和局域接近度的混合修复方法，实验表明此方法的修复效果与贪婪算法基本等同。

Abstract

The invulnerability of complex networks is an important issue which has been widely analyzed in different fields. A lot of works have been done to measure and improve the stability of complex networks when being attacked. Recently, how to recover networks after attack was intensively studied. The existing methods are mainly designed to recover the overall functionality of networks, yet in many real cases the recovery of important nodes should be given priority, to which we refer target recovery. For example, when the cold wave paralyses the railway networks, target recovery means to repair those stations or railways such that the transport capacity of densely-populated cities can be recovered as fast as possible. In this paper, we first compare the impact of attacks on the whole network and target nodes respectively, and then study the efficiency of traditional recovery methods that are proposed based on global centrality metrics. Furthermore, based on target centrality metrics, we introduce a local betweenness recovery method and we find it has better performance than the traditional methods. We finally propose a hybrid recovery method which includes local betweenness metric and local closeness metric. The performance of the hybrid method is shown to be similar to that of the greedy algorithm.

原文链接：https://link.springer.com/article/10.1140%2Fepjb%2Fe2016-70618-0

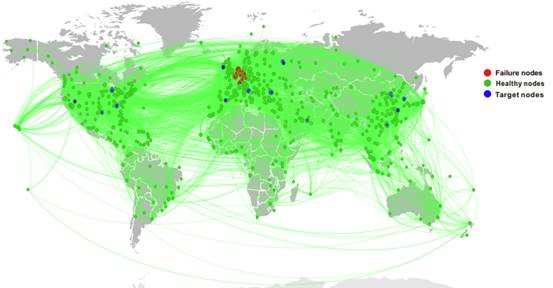
Fig. 1. Illustration of target recovery in complex networks. The network above is world airlines network and the green lines represent the airlines. Red circles, green circles and blue circles correspond to failure nodes, healthy nodes and target nodes respectively.

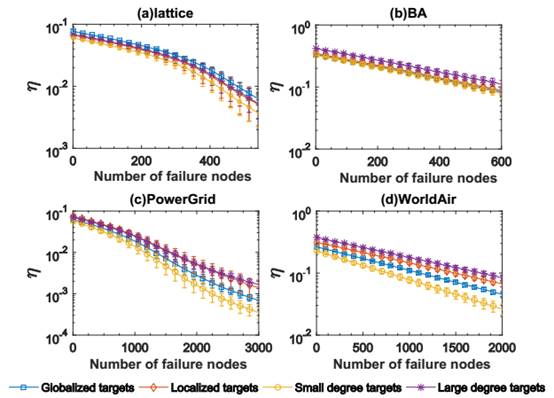
Fig. 2. The dependence of transportation efficiency of four kinds of targets (i.e., globalized targets, localized targets, small degree targets and large degree targets) on the number of failure nodes (random attacks) in different networks (logarithmic coordinate in Y axis).

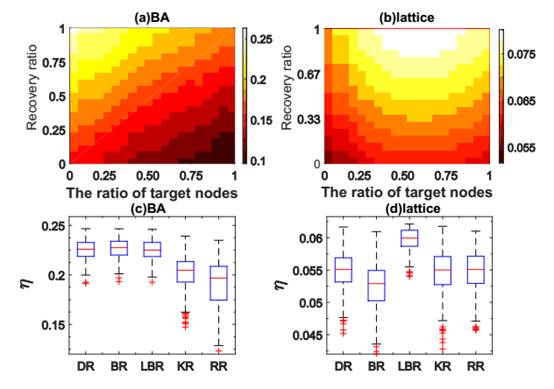
Fig. 3. (a, b) The transportation efficiency with different ratios of target nodes and different random recovery ratios in BA and lattice network respectively; (c, d) the transportation efficiency of target nodes when the network is 20% repaired by different recovery methods in BA and lattice network respectively.

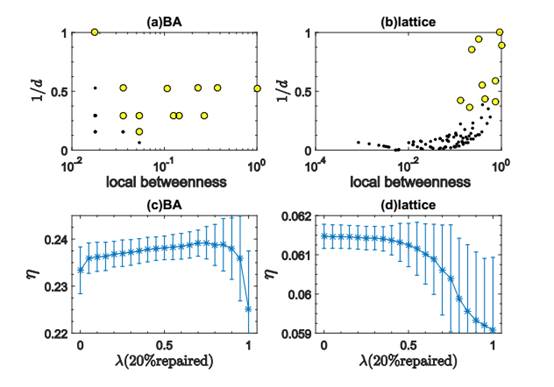
Fig. 4. (a, b) The local betweenness and local closeness of every failure nodes. The yellow circles represent first few repaired nodes in greedy recovery. The black dots stand for the rest of failure nodes (logarithmic coordinate in X axis). (c, d) The dependence of transportation efficiency on hybrid index λ when the network is 20% repaired.

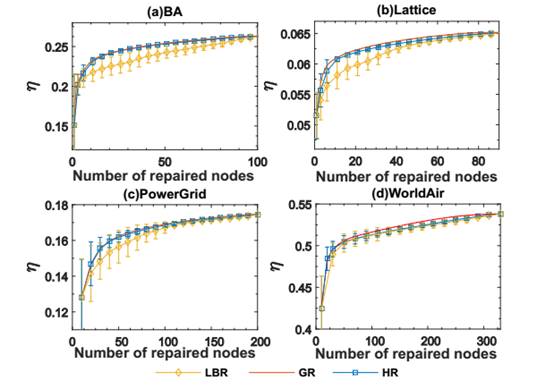
Fig. 5. The recovery effect of local betweenness recovery (LBR), greedy recovery (GR), and hybrid recovery (HR) in BA, lattice, power grid and world air network respectively.

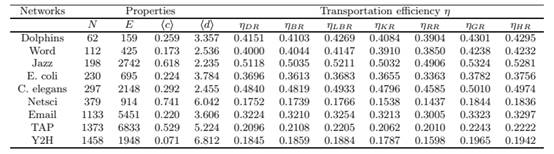
Table 1. The basic structural properties of real networks, and their transportation efficiency η when 20% repaired by different recovery methods. Structural propertes include network size (N), edge number (E), clustering coefficient () and average shortest path length (). We consider seven recovery methods: degree recovery (DR), betweenness recovery (BR), local betweenness recovery (LBR), k-shell recovery (KR), random recovery (RR), greedy recovery (GR), hybrid recovery (HR).