【成果】流体的统计物理与卡门涡街的非平衡相变
流体广泛存在于自然界中。当流速很小的时候,流体分层地流动、互不混合,被称为层流。而当流速很大的时候,层流被破坏,不同流层之间发生混合,形成湍流。由于湍流的混乱性质和不可预测,一百多年来一直吸引着科学家们努力解开其起源和演变的奥秘,卡门涡街是其中一种引人入胜的现象。当流体绕过某些物体时,物体两侧会周期性地脱落出旋转方向相反、有规则双列排列的涡旋。例如水流过桥墩,风吹过高塔、烟囱等,都会形成卡门涡街。1911年,著名科学家冯∙卡门从空气动力学出发找到了这种现象的理论依据,人们后来将这种现象称为卡门涡街。许多研究人员都致力于揭示这种有趣的流动模式的本质。当流体雷诺数较小的时候,绕过物体的流体为层流。随着雷诺数的增加,流体发生层流到卡门涡街的非平衡相变。
精准描述流体的非平衡相变有两方面的巨大挑战。一方面缺乏这样系统的非平衡态理论框架,另一方面涌现出来的相具有空间结构且随时间演化,难以确定其序参量。我们最近发展的系综本征态理论可应对这些挑战。绕开非平衡系统微观态概率分布函数未知的困境,从系统的观测或模拟数据定义微观态并构建其系综。通过系综矩阵的奇异值分解,可得到一组相互独立的本征微观态。原始微观态可表示为本征微观态的加权线性叠加。加权因子为本征微观态的本征值,其平方表示该本征微观态在系综中的权重。当本征值成为有限的时候,对应的本征微观态发生了凝聚,涌现的相由该本征微观态描述,序参量为该本征值。
本文将流体看作由许多格子构成的系统进行研究,采用具有弯曲边界条件的格子玻尔兹曼模拟方法研究流体经过圆柱的流动。由格子的速度和压强模拟数据,我们定义系统的微观态和构造系综,然后计算系统的本征微观态。如图1所示,当雷诺数较小的时候,系统仅有一个层流本征微观态,表明系统完全是层流。当雷诺数大于53.6以后,层流本征微观态的权重变为小于1,同时涌现出一对具有空间结构的本征微观态(见图2)。当雷诺数继续增加到56以后,同时涌现了两对本征微观态,表明卡门涡街实际由三种相叠加而成。为了研究这些相变的属性,本征微观态重整化群理论被应用于研究流体的卡门涡街相变,确立该相变为一级相变。通过分析速度场本征微观态的二维能谱,发现它们在相变点后表现出经典Kolmogorov K41理论的−5/3幂律行为(见图3)。
我们的研究工作表明,本征微观态方法可以用于研究流体系统的集体行为与相变。由于非晶材料与流体存在着一定的共性,未来我们将探索应用本征微观态方法研究非晶材料及其玻璃转变。
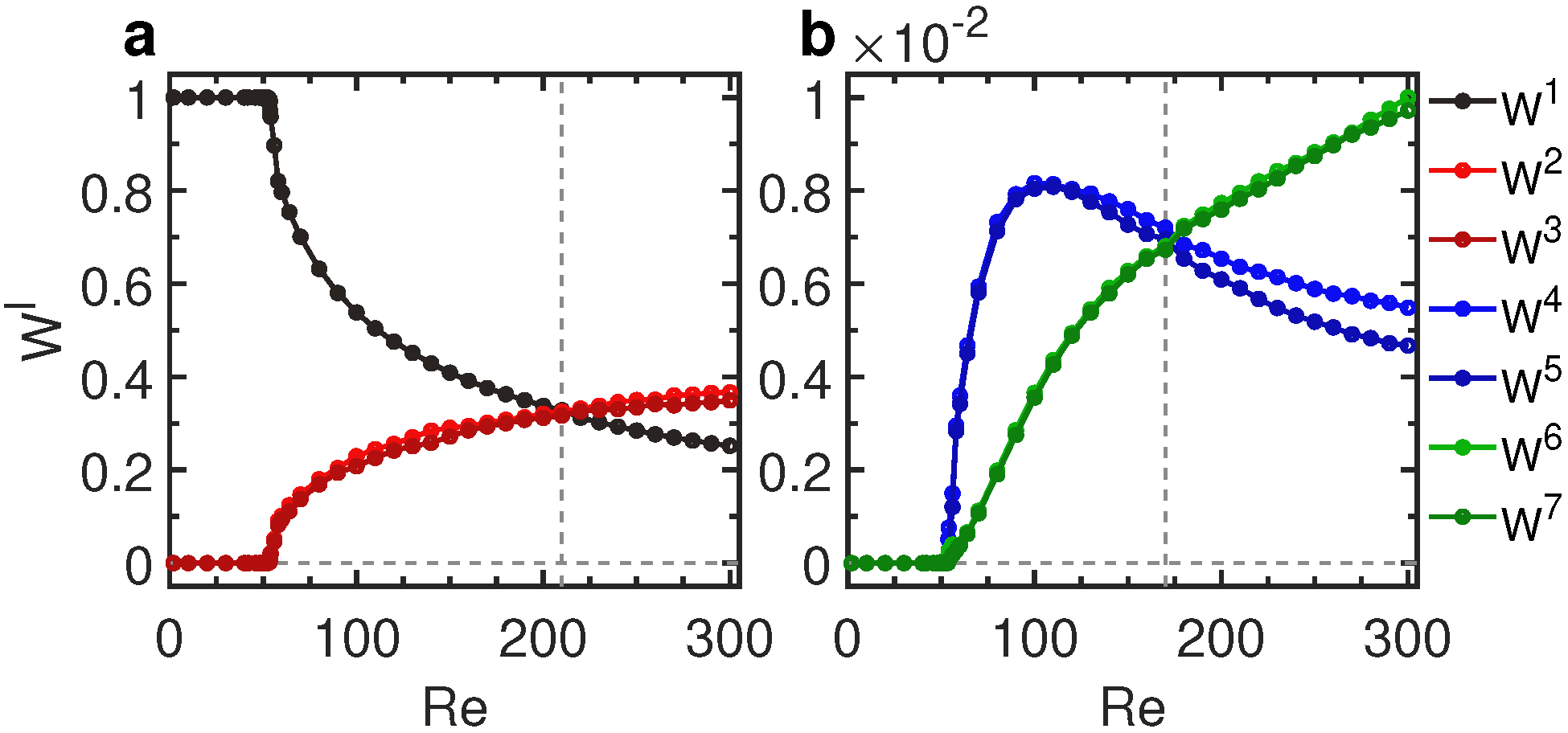
图1:卡门涡街本征微观态的概率与雷诺数的关系。![]() 在图(a)中,
在图(a)中,![]() 在图(b)。不同本征微观态用不同的颜色表示。为了提高可见度,在
在图(b)。不同本征微观态用不同的颜色表示。为了提高可见度,在![]() = 0处包含了灰色虚线。注意,在(a)和(b)的交叉点处,系统的主导本征微观态发生了变化,分别对应于Re = 210和Re = 170。
= 0处包含了灰色虚线。注意,在(a)和(b)的交叉点处,系统的主导本征微观态发生了变化,分别对应于Re = 210和Re = 170。
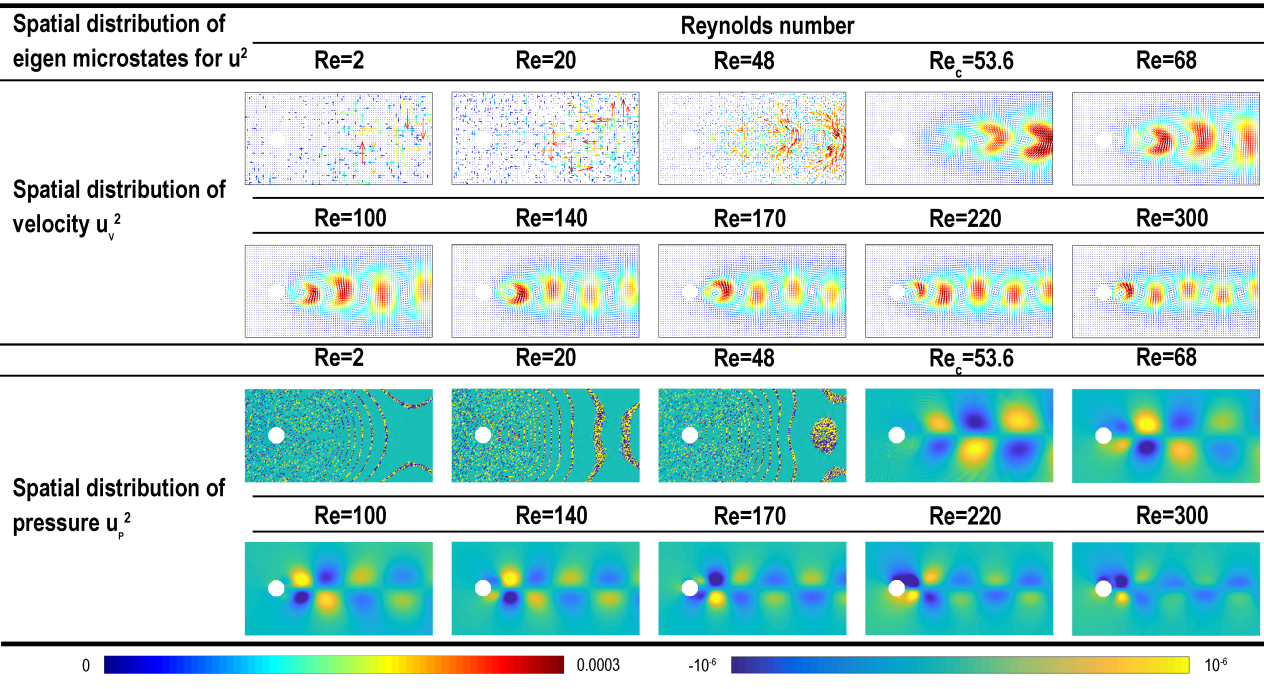
图2:第二本征微观态在不同雷诺数下速度和压力的空间分布。上部是速度的空间分布,用一组箭头表示。箭头方向表示速度方向,颜色表示速度大小,从蓝色(低速)到红色(高速)。下部显示了压力的空间分布,用颜色强度表示,颜色越亮表示压力越高。
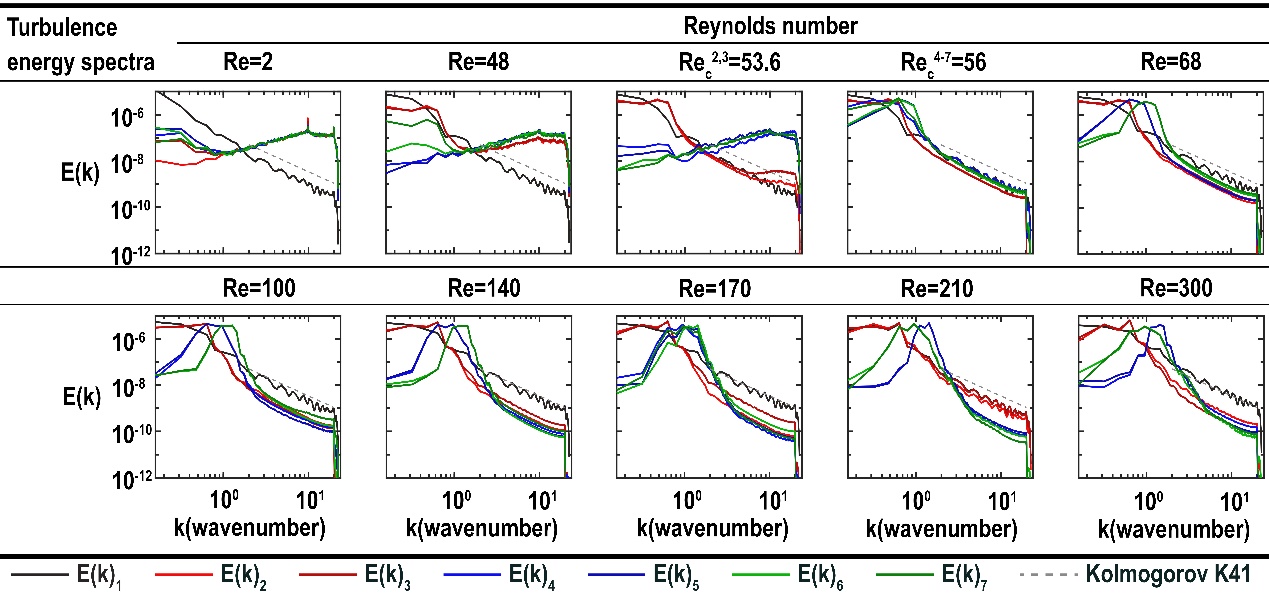
图3:不同雷诺数速度本征微观态的能谱关系。不同本征微观态用不同的颜色表示,灰色虚线代表柯尔莫哥洛夫的K41理论,斜率为-5/3。
该论文以 “Exploring multiple phases and first-order phase transitions in Kármán Vortex Street”为题于2024年8月23日正式发表在SCIENCE CHINA-Physics, Mechanics & Astronomy期刊。bat365中文官方网站博士研究生李旭为论文的第一作者,陈晓松教授和中科院过程所王利民研究员为论文的通讯作者。该论文的研究得到了国家自然科学基金Grant No. 12135003的支持。
论文信息:
Li, X., Xiang, X., Xue, T. et al. Exploring multiple phases and first-order phase transitions in Kármán Vortex Street. Sci. China Phys. Mech. Astron. 67, 110511 (2024).
文章链接:https://doi.org/10.1007/s11433-024-2437-3
供稿:李 旭
编辑:郝林青
审核:李 辉


