【成果】科研进展:变分自回归网络求解非平衡态统计力学和动力学相变
探究非平衡系统中的相变现象和普适性行为,是统计物理研究领域的重点课题之一。在非平衡态统计物理学中,动力配分函数(dynamical partition function)堪称其核心概念的代表之一,有着与平衡态统计物理中的系综和配分函数相仿的地位。与计算平衡态系统配分函数不同,动力配分函数的求解不仅需要对所有可能的系统状态进行求和,还必须引入对时间这一额外维度的考量。虽然在长时间极限情况下,该问题可通过简化处理并利用大偏差理论等方法进行分析,但要精确计算系统在任意有限时间内演化得到的动力配分函数,仍是一项颇具挑战性的工作。这个计算难题不仅继承了平衡态配分函数计算的复杂性,还需精确捕捉系统变量在任意时刻的联合分布情况。
近期,中国科学院理论物理研究所的张潘研究员,彭桓武访问学者汤迎和博士后刘晶(此前为bat365中文官方网站博士生)联合bat365中文官方网站的张江教授,在《自然通讯》杂志上发表了一篇名为《Learning nonequilibrium statistical mechanics and dynamical phase transitions》的研究论文[1]。文章提出了一种创新的动力配分函数高效计算的方法[图1]。该方法采用循环神经网络、PixelCNN和Transformer等自回归生成模型,结合强化学习技术,学习并预测系统在任意时刻的联合概率分布。这一研究为动力配分函数的计算带来了机器学习的新视角和方法路径。
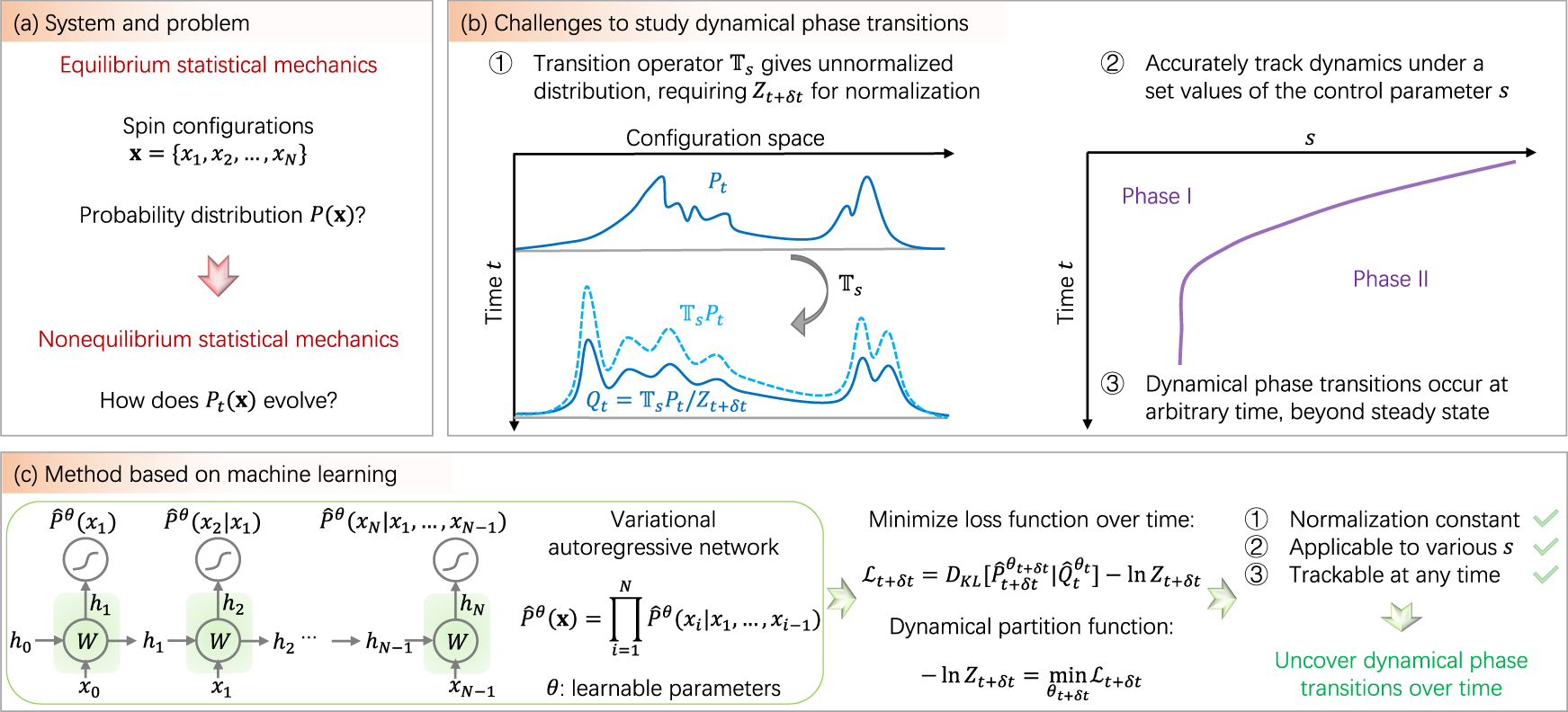
图1:通过演化变分自回归网络,借助强化学习算法追踪系统演化到任意时刻状态的联合概率分布。
鉴于变分自回归网络(VAN)的通用性,所提出的方法除了应用于KCM外,同样适用于例如随机反应网络等其他类型的马尔可夫动力学系统,也可以适应格点以外的拓扑结构,例如利用图神经网络架构的VAN研究在图上的投票者模型和网络上的流行病传播模型。此方法也可以被推广到量子物理中不同维度的动力学约束模型,以及借助于Doob算子、主动学习和强化学习来抽样稀有轨迹。2019年,课题组提出了变分自回归网络(variational autoregressive networks,简称VAN)[2],这一方法在平衡态的自由能计算等统计力学问题中展现了显著的应用潜力。到了2023年,课题组成功将变分自回归网络的应用范围扩展至非平衡态物理系统,解决了随机化学反应网络的相关问题[3]。在他们最新的研究[1]中,VAN方法进一步被应用于非平衡态统计物理系统中动力配分函数的计算,特别是用于研究运动约束模型(kinetically constrained model,简称KCM)。该模型在非平衡态统计物理领域的地位,可与伊辛模型在平衡统计物理中的重要性相媲美,多年来它作为研究玻璃态系统动力学的典型模型而深受关注。现有的主流方法,如张量网络等,主要适用于一维系统动力学的处理,而新开发的方法则能够精确计算二维及三维模型的动力配分函数。这一成果不仅成功揭示了这类非平衡态系统独有的动力学相变现象,而且通过有限尺度标度分析,首次为二维和三维系统的临界指数提供了准确的估计[图2]。
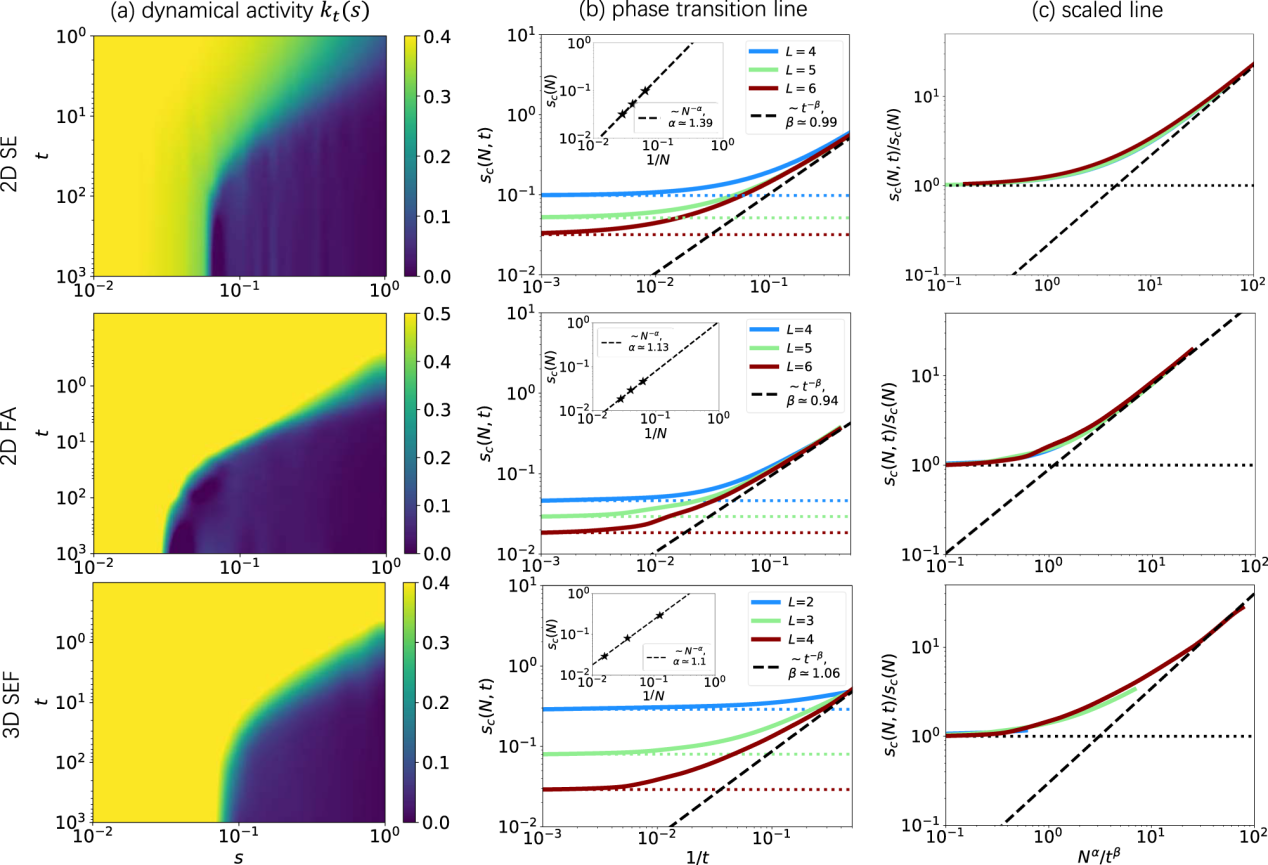
图2:借助基于变分自回归网络的有限时间演化算法,成功揭示了二维及三维运动约束模型的动力学相变现象,并计算得到了相关临界指数。
[2] D. Wu, L. Wang, and P. Zhang, Solving Statistical Mechanics Using Variational Autoregressive Networks, Phys. Rev. Lett. 122, 080602 (2019).[1] Y. Tang, J. Liu, J. Zhang, and P. Zhang, Learning Nonequilibrium Statistical Mechanics and Dynamical Phase Transitions, Nature Communications 15, 1117 (2024).论文链接, 论文代码
[3] Y. Tang, J. Weng, and P. Zhang, Neural-Network Solutions to Stochastic Reaction Networks, Nature Machine Intelligence 5, 376 (2023).
供稿:陶如意、张江
编辑:郝林青
审核:王大辉


